Skip to main content

Top 12 Matlab projects from matlabsolutions.com

Looking for inspiring MATLAB projects to sharpen your skills or impress in your next assignment? At MATLABSolutions.com , we’ve curated the top 12 MATLAB projects that showcase the power of MATLAB in signal processing, image analysis, machine learning, and more. These hands-on examples, complete with code and explanations, are perfect for beginners and advanced users alike. Dive in and explore the best MATLAB projects to elevate your expertise! Signal Smoothing with Moving Average Filter Master signal processing by smoothing noisy data using MATLAB’s movmean function. This project cleans a synthetic sine wave, teaching you noise reduction basics. Ideal for audio or sensor data analysis. Get the code at MATLABSolutions Projects Image Edge Detection Using Canny Filter Explore image processing with MATLAB’s Canny edge detection algorithm. This project highlights edges in any photo, perfect for computer vision applications. Download the script and try it on your own images! Bitcoin Price ...
Post a Comment

How do I generate a unit impulse signal in MATLAB?

Last week I was struggling with my MATLAB Assignment help, and then a good friend told me about MatlabSolutions.com website and they gave me the best Assignment help ever. I hope to always count on the quality and efficiency of your services.
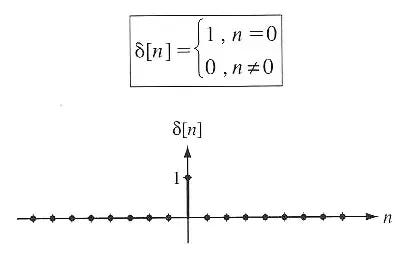
An impulse δ[n] in discrete systems is just a sequence of zeros except at n=0, where its value is 1. It can easily be represented by a vector (or array) in MATLAB.
A continuous impulse δ(t) is a distribution, or generalized function, and it is (in theory) impossible represent it exactly in practice. You can approximate δ(t) with any finite duration pulse with an area equal to 1. The simplest example is a rectangular pulse with width equal to ϵ and height equal to 1/ϵ. To use it in a system, though, you have to set ϵ to a value quite smaller than the shorter time constant of the system where the impulse is being applied. So you need to have some information about the system. Below are examples of several rectangular approximations to an impulse.
Going back to MATLAB, it happens that often you don’t need to create an impulse yourself, because there is an impulse() function which calculates directly the impulse response of a system. See its page, with examples, in Impulse response plot of dynamic system; impulse response data.

Comments

Post a Comment

Popular posts from this blog

https://journals.worldnomads.com/scholarships/story/70330/Worldwide/Dat-shares-his-photos-from-Bhutan https://www.blogger.com/comment.g?blogID=441349916452722960&postID=9118208214656837886&page=2&token=1554200958385 https://todaysinspiration.blogspot.com/2016/08/lp-have-look-at-this-this-is-from.html?showComment=1554201056566#c578424769512920148 https://behaviorpsych.blogspot.com/p/goal-bank.html?showComment=1554201200695 https://billlumaye.blogspot.com/2012/10/tagg-romney-drops-by-bill-show.html?showComment=1550657710334#c7928008051819098612 http://blog.phdays.com/2014/07/review-of-waf-bypass-tasks.html?showComment=1554201301305#c6351671948289526101 http://www.readyshelby.org/blog/gifts-of-preparedness/#comment_form http://www.hanabilkova.svet-stranek.cz/nakup/ http://www.23hq.com/shailendrasingh/photo/21681053 http://blogs.stlawu.edu/jbpcultureandmedia/2013/11/18/blog-entry-10-guns-as-free-speech/comment-page-1443/#comment-198345 https://journals.worldnomads.com...
Post a Comment
Read more

What are some good alternatives to Simulink?

Matlabsolutions provide latest  MatLab Homework Help, MatLab Assignment Help  for students, engineers and researchers in Multiple Branches like ECE, EEE, CSE, Mechanical, Civil with 100% output.Matlab Code for B.E, B.Tech,M.E,M.Tech, Ph.D. Scholars with 100% privacy guaranteed. Get MATLAB projects with source code for your learning and research. SIMULINK is a visual programing environment specially for time transient simulations and ordinary differential equations. Depending on what you need there are plenty of Free, Libre and Open Source Software (FLOSS) available: Modelica language is the most viable alternative and in my opinion it is also a superior option to MathWorks SIMULINK. There are open source implementations  OpenModelica  and  JModelica . One of the main advantages with Modelica that you can code a multidimensional ordinary differential equation with algebraic discrete non-causal equations. With OpenModelica you may create a non-causal model r...
Post a Comment
Read more

USING MACHINE LEARNING CLASSIFICATION ALGORITHMS FOR DETECTING SPAM AND NON-SPAM EMAILS

    ABSTRACT We know the increasing volume of unwanted volume of emails as spam. As per statistical analysis 40% of all messages are spam which about 15.4 billion email for every day and that cost web clients about $355 million every year. Spammers to use a few dubious techniques to defeat the filtering strategies like utilizing irregular sender addresses or potentially add irregular characters to the start or the finish of the message subject line. A particular calculation is at that point used to take in the order rules from these email messages. Machine learning has been contemplated and there are loads of calculations can be used in email filtering. To classify these mails as spam and non-spam mails implementation of machine learning algorithm  such as KNN, SVM, Bayesian classification  and ANN  to develop better filtering tool.   Contents ABSTRACT 2 1. INTRODUCTION 4 1.1 Objective : 5 2. Literature Review 5 2.1. Existing Machine learning techniqu...
Post a Comment
Read more